拜占庭将军问题和区块链技术

         最近经常看到这样的话“区块链技术很好的解决了拜占庭将军问题”，那么什么是拜占庭将军问题，由于东罗马帝国的国土辽阔，其首都是拜占庭，基于防御目的，每个军队都相隔遥远，因此将军间只能靠通信兵传递消息。在战争时，拜占庭帝国军队的将军们必须全体一致的决定是否攻击某一支敌军，因为唯有达成一致的行动才能获致胜利。但将军中若存在叛徒，叛徒可以采取修改消息以欺骗某些将军进行进攻或防守行动，或致使他们无法做出决定，缺乏一致行动的结果则将注定战事的失利，这就是产生了拜占庭将军问题。 

        区块链上分散式网络中节点所出现的任何错误（如，伪造签名、恶意破坏系统的一致性、超时、重复发送消息等）都会导致数据的一致性问题，这就是区块链中存在的拜占庭将军问题。但是，拜占庭将军问题中并不去考虑通信兵是否会被截获或无法传达信息等问题，即消息传递的信道绝无问题。而在消息可能丢失的不可靠信道上试图通过消息传递的方式达到一致性是不可能的。所以拜占庭将军问题是在假定信道没问题的前提下进行一致性和容错性相关研究的，若考虑信道的稳定性问题，就转移到了另一个著名问题“两军”问题上来了，这里姑且不表。 

        无论是Bitcoin的POW还是Ethereum的POS或者Hyperledger的PBFT，共识算法作为区块链技术的核心机制，是无论币圈还是链圈都形成的共识，各共识算法各有优缺点，总体上随着区块链技术的深入以及更多应用和基础平台的涌现，共识算法正处于不断完善和优化的过程中，无所谓优劣，只是适用的场景不同。 这里重点分析一下Hyperledger fbric中的PBFT共识算法。

        PBFT(PracticalByzantine Fault Tolerance)又称实用拜占庭容错算法，前面说了，拜占庭将军问题的解决是建立在通信兵可以正确的传达信息的基础上的，即信道绝对可信，由“两军”问题可以证明理论上可信通道是可以实现的。由拜占庭问题的定义，各方行动的一致性决定了战争的成败，要么一致进攻，要么一致防守，那是否可以理解成拜占庭将军问题本质上是一致性问题呢？答案是否定的，因为可能存在忠诚的将军因为通信兵的叛变而在有利的条件进行没有进行一致性进攻或者在不利条件下都一致没有进攻，所以除了一致性还应考虑正确性的问题。而正确性该如何定义？每一个将军的判断可能都不同，到底谁是正确的呢？这个问题可以转化成每个忠诚的将军都不会因为别的将军因叛徒的干扰而对其忠诚产生怀疑从而不采用他传达的消息，也就是说每个忠诚的将军都能正确的表达自己的意思。所以拜占庭将军问题可以被简化成所有忠诚的将军都能够让别的将军接收到自己的真实意图，并最终一致行动，本质上就是“一致性”和“正确性”的问题。PBFT算法针对的是忠诚的将军，因为叛徒可以做出超出约定的判断，在叛徒的干扰下找到一个抗干扰的算法即是PBFT算法诞生的初衷。

        确保拜占庭将军问题的一致性和正确性主要有三个步骤，预备、准备和确认。

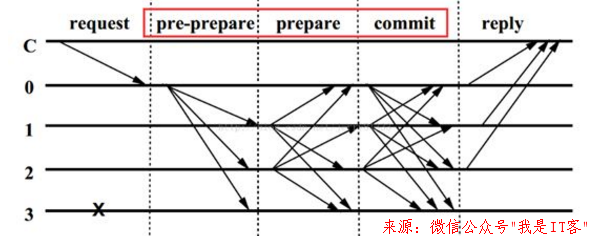
        C为发送请求端，0123为服务端节点，0为主节点，其它为备份节点，3为宕机的服务端节点：

        1. Request：请求端C发送请求到任一服务端节点，假设是0

        2. Pre-Prepare：服务端节点0收到C的请求后进行全网广播，扩散至123

        3. Prepare：123收到广播后记录并再次广播，1广播到023，2广播到013，3因为宕机无法记录也无法广播

        4. Commit：0123节点在Prepare阶段，若收到超过一定数量的相同请求，则进入Commit阶段，并广播Commit请求

        5.Reply：0123节点在Commit阶段，若收到超过一定数量（2F+1【包括自身】）的相同请求，则对C进行反馈

        上述步骤验证了一个公式即R≥3F+1的时候可以确保一致性和正确性，其中R为服务端节点数量，F为有问题的服务端节点数量。只是为什么是3而不是其它数字？笔者从数学角度做了一些简单推演。 

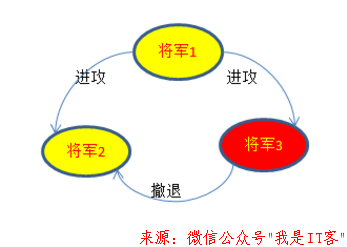
        假设有三个将军（R=3），其中将军3是叛徒（F=1），将军1发送进攻的消息给将军2和将军3，将军3为了破坏一致性，向将军2发送了撤退的消息，那么将军2将无法判断将军1是叛徒还是将军3是叛徒而无法准确做出是进攻还是撤退的判断。可以看出将军1的身份和将军2,3有所不同，类似于司令的角色了，三者的地位等价性被破坏，所以有必要在此前提下做进一步推演。见下图：

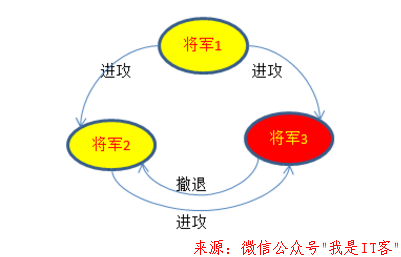
        假设将军1是叛徒，他分别向将军2和将军3发出了进攻和撤退的命令，这时将军2和将军3也会凌乱，二者无法判断将军1是叛徒还是对方是叛徒，行动无法达成一致。这个推演中3<3*1+1，不满足R≥3F+1，所以再次推演下，拜占庭问题无法解决。

        现在把维度提升一阶，令R=4，F=1，R如下图，如果将军4是叛徒，他在收到将军1的进攻消息后为了破坏一致性向将军2和将军3发出了撤退的消息，忠诚的将军2和将军3则分别向对方传达了将军1的进攻消息，那么将军2和将军3均收到2个进攻1个撤退的消息，根据少数服从多数原则，可以判断将军4为叛徒，并做出进攻的一致性行动。见下图：

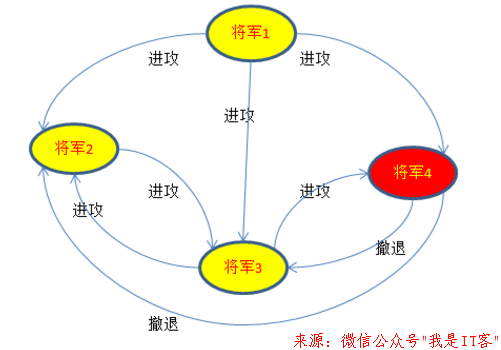
        假设作为司令员的将军1是叛徒，分别向将军2,3,4发出{进攻，进攻，撤退}的指令，那么将军2,3,4最终收到的消息为2次进攻，1次撤退，根据少数服从多数原则，最终采取进攻的行动，将军4可以判读出将军1为叛徒，而将军2和将军3则会把将军4误认为叛徒。这会损坏一些正确性，但是能确保行动的一致性和行动的正确性。

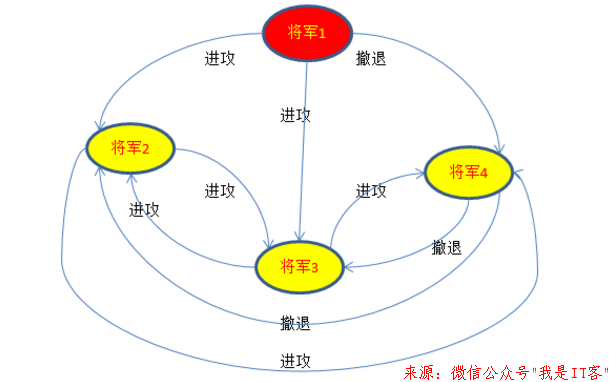
        这个推演4=3*1+1,恰好满足R≥3F+1的边界，继续增加维度的推演同理，有兴趣的朋友可以试一试。至此可以证明系数为3是合理的，其实这个公式符合四模冗余系统的原则，相对于三模冗余系统只能容已知错误结果的静态化情形，四模冗余系统满足了在叛徒做出各种判断的情况下的动态容错要求。就是把自己的命令告诉其他人，并对通过递归算法从其他将军传来的命令取多数的方法来得到自己的结论，可以保证在叛徒数量少于1/3的情况下，忠诚的将军可以实现一致性和正确性要求，据此解决拜占庭将军问题。

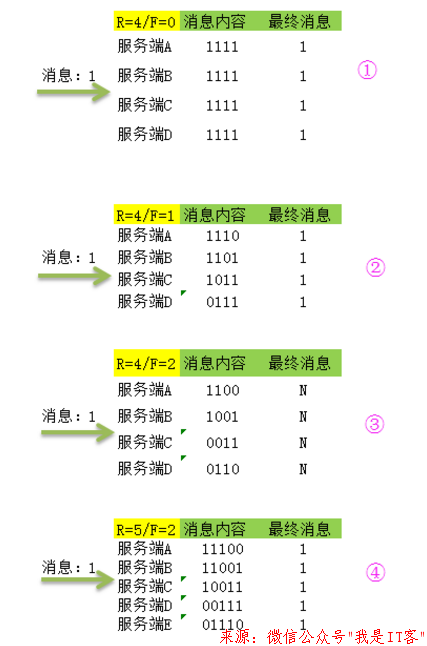
题外话：上图是以二维表的方式展示的实用拜占庭容错算法的部分推算结果，①~③完美表现了R≥3F+1情况下拜占庭容错能够容纳将近1/3的错误节点误差，但是④并不满足R≥3F+1，却仍然达到了最终的一致性和正确性，假设按这种推理的思路，只要F/R小于1/2，结合少数服从多数的原则就可以达到一致性了，这岂不是和PBFT的赖以成立的数学理论基础相悖？！也无笔者把自己绕到沟里了，还请到访的高人指点。